Le 24 octobre 2023 à 11h00 / Amphithéâtre François Canac, LMA
Résumé : Les élastomères appartiennent à la famille des hauts polymères. Microscopiquement, ils se présentent sous forme de macromolécules constituées de longues chaînes de polymères, linéaires ou ramifiées, enchevêtrées les unes dans les autres. Ces macromolécules forment ainsi un réseau tridimensionnel dont les segments de chaînes sont orientés de façon aléatoire.
Compte-tenu de cette structure amorphe et pour des températures supérieures à leur température de transition vitreuse, les élastomères se caractérisent, après leur vulcanisation, par une haute élasticité caoutchoutique.
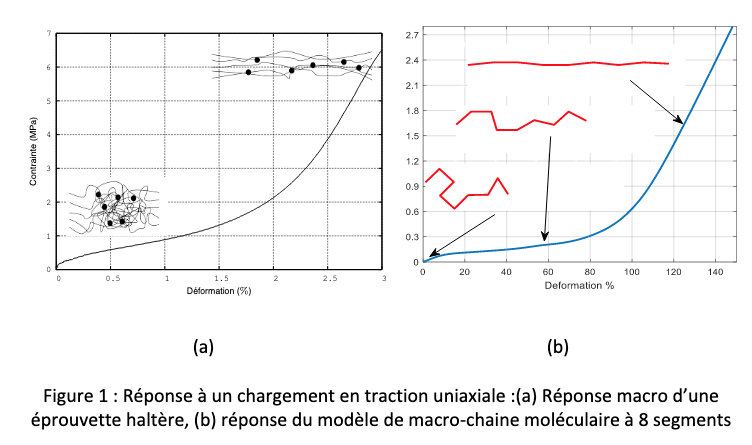
L’élasticité entropique de ces matériaux est le résultat des interactions entre les macromolécules. Ainsi, sous l’action d’une sollicitation mécanique, ces chaînes peuvent glisser les unes sur les autres et changer la configuration microstructurale du réseau moléculaire qui passe d’un arrangement aléatoire à un arrangement orienté suivant la direction de sollicitation (cf Figure 1-a).
Au-delà des modèles phénoménologiques ou statistiques développés depuis les années 1940, de nombreux travaux s’intéressent, ces dernières années, à la modélisation des mécanismes de dépliement des chaines macromoléculaires pour décrire ce comportement. [1,2].
L’objectif de ce séminaire est de proposer une nouvelle modélisation basée sur la configuration. microstructurale du réseau de chaînes macromoléculaires, comportant des points de réticulation et/ou d’enchevêtrement.
A l’échelle du VER, nous supposons que le mécanisme de dépliement des chaines moléculaires est régi par des énergies de déformation des segments de la chaine de Kuhn [3] et des énergies de rotations relatives de ces segments, avec un seuil d’activation. On obtient ainsi un modèle à trois paramètres caractéristiques directement associés aux mécanismes microstructuraux des chaînes.
Les résultats des simulations sur un VER, sous différentes sollicitations à déformation macroscopique imposée (traction uniaxiale, traction biaxiale, cisaillement pur et glissement simple), montrent que le modèle proposé permet de traduire le comportement hyperélatique, des matériaux caoutchoutiques.
Nous aborderons à la fin de l’exposé, une approche visant l’extension du modèle pour simuler les effets de la réticulation des macro-chaines par vulcanisation, mais surtout la simulation des mécanismes irréversibles de rupture de ces ponts de réticulation, dans l’objectifs de traduire l’effet Mullins [4].
[1] E.M. Arruda, M.C. Boyce, A three-dimensional constitutive model for the large stretch behavior off rubber elastic materials, Journal of the Mechanics and Physics of Solids, 1993, 41 (2), pp 389-412
[2] M. Böl, S. Reese, Finite element modeling of rubber-like polymers based on chain statistics, International Journal of Solids and Structures, 2006, 43, pp 2-26.
[3] H. Frielinghaus, Flexible Polymers, in the 35th spring school 2004, “Physics meets Biology – From Soft Matter to cell Biology”, Eds: G. Gompper, U.B. Kaupp, J.K.G. Dhont, D. Ri.
[4] S. Govindjee, J. Simo, A micro-mechanically based continuum damage model for carbon black-filled rubbers incorporating Mullins’ effect, J. Pech. Phys. Solids, 1991, 39, pp 87-112

